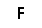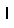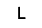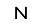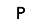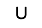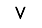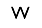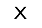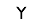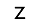About pentominos
Take five identical squares. Arrange the squares so that each square shares at least one edge with at least one of the other four squares. Find all such arrangements, then remove any arrangement that is the same as any another arrangement turned or flipped in any way. In the end there are only 12 distinct arrangements, or pieces.
Each pentomino piece has a single-letter name that, to one degree or another, evokes the shape of that piece:










































































































































































































































































































































































































































































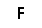

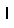

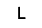

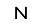

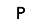



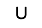

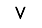

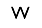

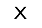

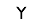

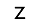



























































About the puzzles
This site examines the four “classic” rectangular pentomino puzzles, some variations of the 8×8 puzzle, and a number of “degenerate” cases, that is, puzzles that are too small to contain all 12 pentominos, such as the 5×5 puzzle.
The goal is to find each and every way to fill the puzzle with the maximum number of pentominos. The number of solutions varies dramatically, from two (for the 3×20 puzzle) to 6951 (for the 5×10 puzzle).
Click on the puzzle’s name or shape to view that puzzle’s home page.
| Puzzle |
Solutions |
Shape |
Notes |
| 3×10 |
145 |
|
A degenerate puzzle. |
| 3×15 |
201 |
|
A degenerate puzzle. |
| 3×20 |
2 |
|
|
| 3×21a |
16 |
|
The dark grey squares represent “holes,” i.e. a region of the puzzle where no piece may be placed.
The 3×21 puzzles each contain three hole squares, reducing the number available squares to the requisite 60. |
| 3×21b |
3 |
|
|
| 3×21c |
1 |
|
|
| 3×21d |
6 |
|
|
| 4×10 |
2085 |
|
A degenerate puzzle. |
| 4×15 |
368 |
|
|
| 4×16a |
146 |
|
The dark grey squares represent holes, i.e. a region of the puzzle where no piece may be placed.
The 4×16 puzzles each contain four holes, reducing the number of available squares to the requisite 60. |
| 4×16b |
56 |
|
|
| 4×16c |
23 |
|
|
| 4×16d |
155 |
|
|
| 4×16e |
18 |
|
|
| 4×16f |
0 |
|
|
| 4×16g |
9 |
|
|
| 4×16h |
14 |
|
|
| 4×16i |
19 |
|
|
| 4×16j |
0 |
|
|
| 4×16k |
47 |
|
|
| 5×3 |
7 |
|
A degenerate puzzle. |
| 5×4 |
50 |
|
A degenerate puzzle. |
| 5×5 |
107 |
|
A degenerate puzzle. |
| 5×6 |
541 |
|
A degenerate puzzle. |
| 5×7 |
1396 |
|
A degenerate puzzle. |
| 5×8 |
3408 |
|
A degenerate puzzle. |
| 5×9 |
5902 |
|
A degenerate puzzle. |
| 5×10 |
6951 |
|
A degenerate puzzle. |
| 5×11 |
4103 |
|
A degenerate puzzle. |
| 5×12 |
1010 |
|
|
| 6×10 |
2339 |
|
|
| 8×8a |
65 |
|
The 8×8 puzzles each contain four holes, reducing the number of available squares to the requisite 60. |
| 8×8b |
21 |
|
|
| 8×8c |
188 |
|
|
| 8×8d |
2170 |
|
|
| 8×8e |
74 |
|
|
| Triplicate F |
125 |
|
In this puzzle, as in the other Triplicate puzzles, the goal is to construct a triple scale of a particular piece using nine of the 11 other pieces.
A degenerate puzzle. |
| Triplicate I |
19 |
|
A degenerate puzzle. |
| Triplicate L |
113 |
|
A degenerate puzzle. |
| Triplicate N |
68 |
|
A degenerate puzzle. |
| Triplicate P |
497 |
|
A degenerate puzzle. |
| Triplicate T |
106 |
|
A degenerate puzzle. |
| Triplicate U |
48 |
|
A degenerate puzzle. |
| Triplicate V |
63 |
|
A degenerate puzzle. |
| Triplicate W |
91 |
|
A degenerate puzzle. |
| Triplicate X |
15 |
|
A degenerate puzzle. |
| Triplicate Y |
86 |
|
A degenerate puzzle. |
| Triplicate Z |
131 |
|
A degenerate puzzle. |
How the solutions are presented
The home page of each non-degenerate puzzle begins with a summary of the unique anchor positions for the puzzle and the number of solutions found for each. Counts are typically displayed at the bottom left corner of a solution.
The rest of each home page is either:
- A depiction of each solution to the puzzle, or
- Links to other pages containing depictions of each solutions to the puzzle. Solutions are collected into groups of 120 or less.
The depiction of a solution usually includes the number of the solution, (the figure to the upper left of the solution), and the number of other solutions related, by some transformation or another, to the solution (the figure to the lower left of the solution):
42
3 |
|
A depiction of solution 42 to the 5×12 puzzle, with a link to a page comparing it with 3 related solutions. |
How the solutions are sequenced
Every solution is given a 60-letter ID by listing, line-by-line from the top-left to the bottom-right, the name of the piece covering each square of the puzzle. The solutions are listed in alphabetical order by ID. Hole squares are indicated by period. For example:
| Solution as displayed |
Solution as alphabetized |
              
              
              
               |
FFWWTTTXZZIIIII
VFFWWTXXXZYYYYP
VFNNWTUXUZZYLPP
VVVNNNUUULLLLPP |
       
       
       
       
       
       
       
        |
IIIIIFNL
UUXFFFNL
UXXXFNNL
UUX..NLL
PPP..VVV
TPPWWZZV
TTTYWWZV
TYYYYWZZ |
Locating a particular solution
Rotate and/or flip your solution until the piece filling the upper-left square is the lowest in alphabetical order. If there is a choice, continue flipping and rotating until the second, third and following squares are filled by the pieces lowest in the sort sequence.
|
              
              
              
               |
In this solution, the choices for the first and second squares are LL, LU, VV and YY. The upper solution must be rotated 180° to bring the preferred solution, (i.e. the LL) to the upper-left corner. |
              
              
              
               |
About the transformations
The program compares every pair of solutions for each puzzle to see if they are related. In particular, it looks for three kinds of similarity: reflections, rotations, and rearrangements.
| Rx: Reflect a single, connected group of pieces in the horizontal (X) axis |
              
              
              
               |
Here, the P and Y pieces are turned over top-to-bottom, like resetting an hourglass. |
              
              
              
               |
| Ry: Reflect a single, connected group of pieces in the vertical (Y) axis |
              
              
              
               |
Here the L and P pieces are turned over left-to-right, like turning a page. |
              
              
              
               |
| Rd: Reflect a single, connected group of pieces in the diagonal axis |
              
              
              
               |
Here, the L and U pieces are turned over along the diagonal running from the lower left to the upper right, like the motion your left hand makes when look at your palm, then flip your hand over. |
              
              
              
               |
| Ra: Reflect a single, connected group of pieces in the antidiagonal axis |
              
              
              
               |
Here, the P and T pieces are turned over along the antidiagonal running from the upper left to the lower right, like the motion your right hand makes when look at your palm, then flip your hand over. |
              
              
              
               |
| Sw: Swap two subgroups within a single, connected group of pieces |
              
              
              
               |
In this example, the two-piece (P and Z) subgroup swaps position with the two-piece (F and U) subgroup. This transformation can also be thought of as a rearrangement of the four-piece (F, P, U and Z) group.
Swap transformations include cases, like this one, where the two subgroups being swapped are also reflected or rotated during the swap. Here, each subgroup is reflected in the antidiagonal axis as part of the swap. |
              
              
              
               |
| T1: Rotate (turn) a square, connected group of pieces by 90° clockwise |
           
           
           
           
            |
This transformation, along with the T3 transformation, is rather rare. For a group of pieces to be rotatable by 90° the area it covers must be a square and a multiple of five: The only candidate is the 5×5 square.
|
           
           
           
           
            |
| T2: Rotate (turn) a single, connected group of pieces by 180° |
                   
                   
                    |
Here, the two solutions to the 3×15 3×20 puzzle are the same but for the 180° rotation of the seven-piece (F, L, N, T, W, Y and Z) group.
My thanks to Przemyslaw Remin for reporting my mistake. |
                   
                   
                    |
| T3: Rotate (turn) a square, connected group of pieces by 90° counterclockwise |
           
           
           
           
            |
This transformation, along with the T1 transformation, is rather rare. For a group of pieces to be rotatable by 90° the area it covers must be a square and a multiple of five: The only candidate is the 5×5 square.
|
           
           
           
           
            |
| Ar: Rearrange a group of pieces |
              
              
              
               |
This is the most general sort of transformation, and the default designation if a transformation cannot be otherwise classified.
In this frequently occurring case the F and N pieces fill the same patch of the puzzle in two ways, yet there is no rotational or reflectional symmetry between the two. |
              
              
              
               |
         
         
         
         
         
          |
The only other kind of two-piece, in-place rearrangement without reflectional or rotational symmetry is the one shown here involving the L and P pieces. There are, of course, very many in-place rearrangements of three or more pieces. |
         
         
         
         
         
          |
| Ex: Exchange one group of pieces for another group |
         
         
         
         
          |
Exchange transformations occur only with degenerate puzzles (i.e. those that involve less than the full complement of 12 pentominos.)
In this case, the area of the solution occupied by the pair I and P can also be occupied by the pair P and Z.
As this example shows, the two sets of pieces need not be disjoint; here the P piece occurs in each solution, albeit in a different position. |
         
         
         
         
         
|
| Rx*: Reflect a disconnected group of pieces in the horizontal (X) axis |
         
         
         
         
         
          |
Here, the two-part, four-piece (L, N, T and Y) group is reflected in the horizontal axis. Interestingly, this is the only disconnected horizontal reflection found in any of the four rectangular puzzles. It occurs only in the 6×10 puzzle, and only twice. |
         
         
         
         
         
          |
| Ry*: Reflect a disconnected group of pieces in the vertical (Y) axis |
              
              
              
               |
Here, the two-part, four-piece (F, L, P and Z) group is reflected in the vertical axis. It can be also be viewed as the reflection in the vertical axis of the connected five-piece (F, I, L, P and Z) group. |
              
              
              
               |
| Rd*: Reflect a disconnected group of pieces in the diagonal axis |
       
       
       
       
       
       
       
        |
Here the two-part, four-piece (I, L, N and W) group is reflected in the diagonal axis. This is one of only six disconnected reflections in the diagonal axis, all found in the 8×8d puzzle. |
       
       
       
       
       
       
       
        |
| Ra*: Reflect a disconnected group of pieces in the antidiagonal axis |
         
         
         
         
         
          |
This can be viewed as two distinct transformations:
- The reflection of the F and P-pieces in the antidiagonal axis, and
- The reflection of the I and L-pieces in the antidiagonal axis.
Or, it can be viewed as the reflection in the antidiagonal axis of the two-part, four-piece (F, I, L and P) group.
Finally, it can be seen as the reflection of the connected, five-piece (F, I, L, P and X) group. |
         
         
         
         
         
          |
| Sw*: Swap the positions of two separate groups of pieces |
              
              
              
               |
In this example the two-piece (N and Z) subgroup swaps position with the two-piece (P and T) subgroup. |
              
              
              
               |
| T2*: Rotate (turn) a disconnected group of pieces by 180° |
              
              
              
               |
Here, the two-part, four-piece (P, W, Y, Z) group is rotated 180°. |
              
              
              
               |
| Ar*: Rearrange a disconnected group of pieces |
              
              
              
               |
These solutions show how a two-part, four-piece (F, P, T and Z) group can be rearranged to yield distinct solutions. This is similar to a disconnected swap transformation, except that here pieces may be recombined (i.e. jump from one group to another). In a disconnected swap transformation the pieces within each group stay together. |
              
              
              
               |
| Ex*: Exchange a disconnected group of pieces for another disconnected group |
         
         
         
         
          |
Exchange transformations are occur only for degenerate puzzles (i.e. those that involve less than the full complement of 12 pentominos.)
In this case, the areas of the solution occupied by the F, I, L, P, U pieces can also be occupied by the F, I, L, V, Z pieces.
As this example shows, the two sets of pieces need not be disjoint; here the F, I and L pieces occurs in each solution, albeit in different positions. |
         
         
         
         
          |
About the program
The program is written in C#. It begins by finding the unique locations for the anchor piece. The X-piece is used for the anchor because it is the only piece that has a unique orientation (i.e. is the same no matter how it is reflected or rotated). Careful placement of the anchor piece reduces the number of duplicate solutions produced (i.e. a solution that is a reflection or rotation of another solution) which in turn decreases the length of time needed to find all a puzzle’s solutions.
For each position of the anchor piece the program tries to fit the remaining pieces around the anchor within the frame of the puzzle. The algorithm is a very straight-forward recursive one.
Each solution is checked to make sure it is unique. Limiting the location of anchor piece eliminates most of these automatically. But, when the anchor piece lies along the vertical or horizontal axis, the program will find solutions that are reflections of each other. In that case the solution that occurs first in the sort order is retained and the other discarded.
Limitations of the program
The program uses a very unsophisticated method of finding connections between solutions: it simply examines every possible pair of solutions and makes note of the differences between them. It tries to classify the connections by detecting reflections, 90° (quarter-turn), 180° (half-turn), 270° (three quarter-turn) rotations, and swaps. Failing that, it reports all general rearrangements involving six pieces or less.
There is one class of connection that is undetected by the program but plain to any observer. Consider these two solutions to the 5×12 puzzle:
           
           
           
           
            |
These two solutions can be viewed as identical except for the position of the I piece. However, the program sees only that all twelve pieces are in different positions. Hence, no connection is reported.
|
           
           
           
           
            |
There is another kind of connection the program misses. Because it puts each solution in its canonical order before comparing pairs of solution, it fails to recognize connections that require a reflection and/or rotation of one of the solutions being compared.
Thanks to Sergio Gon
In Nov 2011 Mr. Sergio Gon, a Texas school teacher, told me how a chance encounter with a set of plastic puzzle pieces marked the beginning of his ongoing interest with pentominos.
Sergio has developed an elegant technique for transforming the solutions posted here as lines in a text file into coloured, graphical depictions using the spreadsheet program Microsoft Excel. He explains his technique below. Note it is helpful to have the spreadsheet (or this very large webpage rendition) in view while you read.
- Copy one of the solutions found here, the 4×15 for example, to column B as block of text.
- Separate each letter into its own cell—to do this faster you can use
the MID formula (this formula returns a specific number of characters from a
text string, starting at the position you specify, based on the number of
characters you specify.) so, we are using this help to have each letter
separated in one cell, you can see the results in range C3:BS3.
- Add conditional formatting to the range C3:BS3 so each cell
changes colour depending on the letter value inside the cell.
- Copy each group of 15 cells in the correspondent order
one over the other to have the solution in colour.
- For printing, select
the desired range (in this case range BU3:EU371) to fit it on four pages.
More recently, in February 2012, Sergio has refined and improved his technique producing spectacular solutions for the 6×10 and 8×8d puzzles. My apologies to Sergio for having taken over four months to post this.
Thanks to David Ball
In June 2010 I spent a delightful afternoon with fellow pentomino enthusiast David Ball of Vancouver. David had been a tireless and methodical pentomino researcher for many years, and had amassed a stack of notebooks chronicling his findings. These he has generously placed in my care, along with his unique collection of pentomino artifacts and ephemera. I hope to one day incorporate David's collection into this website. For now, I wish to thank David for his generosity and trust.
In February 2011 David alerted me to the work of George Peter Jelliss who has painstaking compiled and decoded pentomino puzzles from the celebrated Fairy Chess Review (FCR). What makes this especially valuable is that FCR employed a peculiar notation for pentomino arrangements that is indecipherable without the key. Mr. Jelliss has transcribed these into the now familiar graphic depictions of this kind used here.
Thanks, again, to Sam and Irene
In April 2011 I received a lovely message from Sam and Irene regarding the site. Irene very thoughtfully included a diagram of related solutions to the 5×12 puzzle which are missing from this enumeration because of limitations in the program.
A scant month later (May 2011) Samantha and Irene have again demonstrated a computer (read, this coder) is no match for their dogged determination and perseverance. This time Irene has examined the 4×15 puzzle, rendering another impressive diagram of related solutions to the 4×15 puzzle missing from this site.
Acknowledgements
The solutions to the puzzles listed here match other published results, in particular those by Gerard Putter and Lars Kindermann. Kindermann provides all the solutions to the four classic puzzles. He has ordered the solutions differently from order used here, making a direct comparison rather cumbersome.
Analysis of the connections within the solutions to a puzzle has been done by others, including the anonymous author of Pentomino Relationships. The definitive print work remains Polyominoes by Solomon Golomb.
Feedback
I’d like to hear what you think of this site. Please send your comments to Steve Chapman.
Page updated 24 Aug 2022 · Website by